Tutoriel 14 : De l'intelligence dans les objets
Date de publication : Lundi 18 mars 2003 , Date de mise à jour : Lundi 4 février 2008
Par
Gilbert Miralles (gilmir.developpez.com)
De l'intelligence dans les objets
Je souhaitais continuer ces Tutoriels avec une approche du processus de l'intelligence artificielle qui est contrairement aux idées reçues relativement simple.
Sans rentrer dans les algorithmes compliqués, on peut développer des jeux simples comme Le bandit Manchot" ou bien un jeu de "Morpions".
Historiquement l'Intelligence artificielle est aussi vieille que le concept de jeu vidéo
Quand les amateurs commencent à écrire leurs propres programmes, beaucoup rêvent du jour où ils seront capables de programmer un jeu d'échecs ?
Mais l'écriture d'un jeu d'échecs tourne parfois à l'obsession, même parmi les programmeurs les plus érudits et même familiarisés avec les échecs.
Il convient de ne pas perdre de vue que ces jeux n'ont que peu de choses à voir avec les jeux d'arcades, d'aventures ou de simulations, qui tous demandent des techniques différentes de programmation et de l'imagination dans les procédures d'adresses.
Nous commencerons cette analyse des jeux "Intelligents" avec un exemple que d'aucuns trouverons un peu simpliste, mais qui a l'avantage de recouvrir la plupart des principes
d'écriture de ces jeux.
Si vous avez étudié les fonctions aléatoires, vous avez appris que générer une séquence réellement aléatoire est une tache impossible pour les êtres humain et pour les ordinateurs, bien que ces derniers arrivent à faire une meilleure approximation.
Dans une longue série de coups, le joueur humain choisit invariablement un objet plus souvent que les autres. On peut donc inscrire dans le programme un sous programme qui garde en mémoire les choix du joueur en utilisant un tableau à trois éléments que l'on pourrait appeler :
Choix1, Choix2, Choix3.
L'ordinateur peut alors calculer quel objet est le plus souvent joué, et ensuite jouer l'objet qui
l'emporte sur celui-ci.
Le plus grave inconvénient de cet algorithme apparaît au moment où le joueur réussit à percer la stratégie de l'ordinateur.
Les êtres humains sont incapables de prendre une décision totalement irrationnelle ou aléatoire. Il s'ensuit que chaque choix dépend des choix précédents.
Si l'ordinateur réussit à élaborer une approximation sur ces choix, alors il devrait pouvoir gagner assez régulièrement
Le programme doit être écrit de telle façon qu'il puisse interpréter la formule pendant le déroulement de la partie.
Les programmes qui sont capables d'apprendre de cette façon s'appellent :
Des programmes "Heuristiques"
Un programme heuristique permet à l'ordinateur de détecter des changements dans la stratégie de son adversaire et de modifier son algorithme en conséquence.
Il applique une technique statistique appelée "Corrélation"
Nous allons faire abstraction de toutes ces techniques rébarbatives pour nous consacrer à
l'étude simpliste d'un jeu de morpions, tout en sachant que nous aurons par la suite la possibilité d'améliorer ses performances en suivant les techniques décrites précédemment.
 |
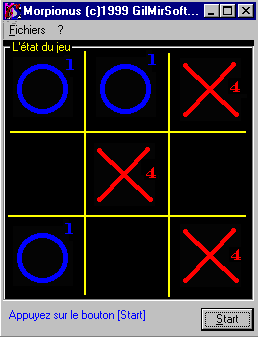
Une évaluation correcte des positions est fondamentale à tout programme de jeu même si ce jeu est aussi simple que le morpion. Sur ce tableau 3x3 les zéros du joueur sont représentés par le chiffre1, les croix de l'ordinateur par le chiiffre4. A l'aide de ces chiffres, on peut évaluer n'importe quelle situation de jeu.
Il suffit de faire les totaux pour chaque rangée, colonne, diagonale. Un total de 12 indique que l'ordinateur peut donc gagner, et un total de 3 que c'est le joueur qui est sur le point de conclure. Les valeurs 1 et 4 sont utilisés parce qu'elles fournissent des totaux différents pour chaque combinaison de coup. Dans le cas de cette figure, c'est celui qui va jouer le premier qui va gagner puisqu'il va aligner (12) ou (3).
|
Il est souhaitable de faire simple dans un premier temps, mais il m'apparaît indispensable
d'utiliser un générateur aléatoire pour générer le carré de départ lorsque c'est à l'ordinateur de jouer. Cela désoriente le joueur(un certain temps) qui ne sait pas ou le computer va positionner son pion.
On pourrait choisir un algorithme compliqué de façon que l'on ne tombe pas sur des chiffres déjà utilisés tout au moins dans la limite des 9 disponibles.
Mais faisons simple , et l'on pourrait coder le générateur sous la forme de :
Private Sub Form_Load( )
CenterForm Me
Form1!ctlQuiJoue.Caption = "Appuyez sur le bouton [Start]"
Randomize
End Sub
Sub Ordi_A_Jouer ( )
Valeur% = Int(Rnd * 9)
Form1!Label10.Caption = Valeur%
|
le programme a sélectionné une case, contrôler si la case Index est vide puis,
affichons la case choisie.
(1)
If Form1!ctlControlEtat(Index).Caption = "0" Then
Form1!Image1(Valeur%).Picture = Form2!Image_X.Picture
Form1!ctlControlSelect.Caption = Valeur%
Iteration_Compteur_Ordi
Exit Sub
Else
Control_Resultat
End If
End Sub
|
Prochain tutoriel :
 |
Le débogage
|
| (1) |
Il est évident que la première fois, la case est vide, nous aurions pu créer un traitement conditionnel pour aiguiller sur les instructions adéquates uniquement pour le premier mouvement du jeu, ou bien nous aurions pu créer un procédure supplémentaire.
|
Copyright © 2000 Gilmir. Aucune reproduction, même partielle, ne peut être faite
de ce site et de l'ensemble de son contenu : textes, documents, images, etc
sans l'autorisation expresse de l'auteur.
Sinon vous encourez selon la loi jusqu'à 3 ans de prison et jusqu'à 300 000 E
de dommages et intérêts.
Cette page est déposée à la
SACD.
